The Product Rule Online Notes- Math Help and Tutoring

Need one-on-one tutoring with me? I teach all of this material! Contact me for a quick response on your needs.
Want my FULL version of these notes with more worked examples and help? Click here.

Introduction

Thus far we have looked at differentiating functions using the definition of the derivative as well as with the power rule of differentiation. We also looked at the linearity of the derivative operator, meaning we could also tackle sums and differences of these power functions, such as $f(x) = 3x^4+12x^2-9x$ . We simply take the derivatives of the individual terms here, and add the results.

However, this does not work with multiplication. In words, the derivative of a product of functions does not equal the product of their individual derivatives. In math,

(1) $\begin{equation*} \diff{}{x} \Big[f(x) \cdot g(x)\Big] \neq f'(x) \cdot g'(x) \end{equation*}$

You can show that this doesn’t work by considering the function $f(x) = x \cdot x^3$ . This is a product of individual functions as mentioned above. This function is simply equal to $x^4$ , so the derivative should be $f'(x) = 4x^3$ . What if we go back to the original $x \cdot x^3$ and take the derivative of $x$ and $x^3$ separately, and multiply them together? We would get $1 \cdot 3x^2$ , which we can see is clearly not the derivative we know it should be $(4x^3).$ Clearly we have validated the non-equality of Equation 1.

It turns out that the derivative of a product is a little more complicated than this, but not by much! I provide the following product rule of differentiation without proof:

(2) $\begin{align*} \diff{}{x}\Big[f(x) \cdot g(x)\Big] = f'(x) \cdot g(x) + f(x) \cdot g'(x) && \text{(Product Rule)} \end{align*}$

(3) $\begin{equation*} \diff{}{x}\Big[f(x) \cdot g(x)\Big] = f'(x) \cdot g(x) + f(x) \cdot g'(x) } \end{equation*}$

(Product Rule)

Using this rule always entails thinking about the pattern rather than the function names, such as “last d first plus first d last”, where I rearranged the order of saying the first part even though the result is the same, and “d” implies derivative. Also notice this result is perfectly reversible; you can do either part first because they’re added together, so just make sure you end up with two terms, each of which has one of the derivatives. Let’s look at implementing the product rule!

Example 1

Let $h(x) = x \cdot x^3$ like in our example above. Show that the derivative ends up being the expected $4x^3$ with the product rule.

In the above example, if we lay out our function over the formula for the product rule, we have that $f(x) = x$ and $g(x) = x^3$ . Therefore the derivative of this product is given as follows:

$h'(x) = f'(x) \cdot g(x) + f(x) \cdot g'(x)$

$= (1)(x^3) + (x)(3x^2)$

$= x^3 + 3x^3 = 4x^3$

as expected since $h(x)$ is simply $x^4$ !

When the product rule isn’t needed

We didn’t need to use the product rule for the above example. Even though the product rule is always true for any two functions, here are two situations where we don’t need to use it:

One of the “functions” is a simple constant (constants can be pulled out of the derivative operator), such as with 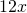$12x$ or $32x^2$ .
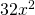If you can simply multiply the two functions together and take the derivative of what results, such as with 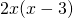$2x(x-3)$ and $(9x^2-1)(4x+1)$ .

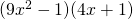There are indeed various situations where you have no choice but to use the product rule because the factors don’t combine, such as in the functions $y = x\sqrt{x-2}$ , $y = \sin x\cos \sqrt{x}$ , $y = x^2 \ln (x)$ , and $y = x^3 e^x$ .

Example 2

Find the derivative of $f(x) = 4x(x^2-3x^3)$ , first by multiplying the factors together and differentiating without the product rule, and then by using the product rule and simplifying the answer.

Note that the $f(x)$ given in this problem has nothing to do with the $f(x)$ in the power rule. You’ll have to keep them separate in your work and in your mind while completing the product rule. Now, note that this is another example where we don’t necessarily need the product rule, because we can distribute the first term into the parenthesis to eliminate the product, as follows.

$f(x) = 4x^3 - 12x^4, \; f'(x) = 12x^2 - 48x^3$

However, the product rule is always correct, and neither of the factors is just a constant, so let’s employ it. Now, you’ll often come across problems that call the overall composite function $f(x)$ , for example. So when employing the product rule (in which I called $f(x)$ the first factor, not the overall function), always be thinking about “first” and “last” functions, not f(x) and g(x). It just makes it simpler to think about.

The derivative with the product rule is then:

$f'(x) = (4)(x^2 - 3x^3) + (4x)(2x-9x^2)$

$= 4x^2 - 12x^3 + 8x^2 -36x^3$

$= 12x^2 - 48x^3$

just like before!

Example 3

Find $\diff{y}{x}$ where $y = (3x+1)(4x-2)$

The product rule is as follows:

$\diff{y}{x} = \diff{}{x} \Big[ 3x+1 \Big] \cdot (4x-2) + (3x+1) \cdot \diff{}{x} \Big[ 4x - 2 \Big]$

$= (3)(4x-2) + (3x+1)(4)$

$= 24x - 2$

which you can verify by foiling out y(x) and taking the derivative of the pieces.

Example 4

Find $f'(x)$ where $f(x) = 3x^4(5x-1)$

We’ll call the first function $3x^4$ , including the 3, even though we could also pull the 3 entirely out of the derivative with the same results.

$f'(x) = \diff{}{x} \Big[ 3x^4 \Big] \cdot (5x-1) + (3x^4) \cdot \diff{}{x} \Big[ 5x -1 \Big]$

$= (12x^3)(5x-1) + (3x^4)(5)$

$= 75x^4 - 12x^3$

which you can verify by foiling out y(x) and taking the derivative of the pieces.

Example 5

Find the derivative of $g(x) = 3x^2\sqrt{x-3}$ .

This is clearly a product of functions. However, notice here that we can’t easily distribute the first part into the radical, so we use the product rule:

$g'(x) = \diff{}{x}\Big[3x^2\Big] \cdot \sqrt{x-3} + 3x^2 \cdot \diff{}{x} \Big[(x-3)^{1/2}\Big]$

$= 6x\sqrt{x-3} + 3x^2 \cdot \Big[\frac{1}{2} (x-3)^{-1/2} \Big] = \textcolor{Magenta}{6x\sqrt{x-3} + \frac{3x^2}{2\sqrt{x-3}}}$

$= \frac{12x(x-3)}{2\sqrt{x-3}} + \frac{3x^2}{2\sqrt{x-3}} = \textcolor{Magenta}{\frac{15x^2 -36x}{2\sqrt{x-3}}}$

where the last line included finding a common denominator and adding the fractions (only algebra here, no calculus), although either colored expression is an acceptable final answer.

Distributing?

It turns out this problem can be performed without the product rule as well, although there are still many problems that cannot be handled in this way. Notice that $x^2 = \sqrt{x^4}$ . Therefore,

$g(x) = 3\sqrt{x^4}\sqrt{x-3} = 3\sqrt{x^5 - 3x^4}$

and now there’s no product! The derivative proceeds with the chain rule. Ignore this approach if you haven’t yet done the chain rule.

$g'(x) = 3 \cdot \frac{1}{2} (x^5 - 3x^4)^{-1/2} \cdot (5x^4 - 12x^3)$

where the last term is from the chain rule. This simplifies to what we got before as follows:

$= \frac{15x^4 - 36x^3}{2\sqrt{x^5 - 3x^4}} = \frac{15x^4 - 36x^3}{2\sqrt{x^4} \sqrt{x - 3}} = \frac{15x^2 -36x}{2\sqrt{x-3}}.$

More Product Rule Examples

The following are more examples of using the product rule with special functions and the chain rule, which are only covered later on in these notes. These problems only apply after you’ve done some future material as well.