The Quotient Rule

  • Need one-on-one tutoring with me? I teach all of this material! Contact me for a quick response on your needs.
  • Want my FULL version of these notes with more worked examples and help? Click here.

Introduction

We looked at how to take the derivative of a product of functions using the product rule, which showed that the derivative of a product of functions is not simply the product of the individual derivatives. The same goes for quotients of functions (not surprisingly, because division is simply multiplication by the inverse of the denominator). In words, the derivative of a quotient of functions does not equal the quotient of their individual derivatives. In math,

(1)   \begin{equation*} \diff{}{x}\Big[\frac{f(x)}{g(x)}\Big] \neq \frac{f'(x)}{g'(x)} \end{equation*}

It turns out that we can determine what the derivative of a quotient is based on what we know from the product rule, by rewriting the quotient of functions \frac{f(x)}{g(x)} as a product f(x) \cdot [g(x)]^{-1} where [g(x)]^{-1} represents the reciprocal of the original denominator, g(x). Check out my full notes on this section for a detailed usage of the product rule to complete this derivation. When performed and simplified, we find the following, called the the quotient rule of differentiation.

Always say “derivative of top times bottom, minus top times derivative of bottom, all over bottom squared” when utilizing this formula rather than thinking of function names.

When the Quotient rule isn’t needed

Even though the quotient rule is always true for any two functions, here are two situations where we don’t need to use it, just like with the product rule:

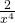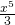  • One of the “functions” (top or bottom) is a simple constant (constants can be pulled out of the derivative operator), such as with \frac{2}{x^4} or \frac{x^5}{3} (see examples below).
  • If the denominator can be distributed across the terms of the numerator, thus eliminating the fraction altogether, such as with 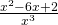\frac{x^2 - 6x+2}{x^3} (see example below).

There is also the possibility of rewriting the fractional function as a product of two functions and using the product rule instead, such as with \frac{\sin{x}}{x^2} being rewritten as (\sin{x}) \cdot (x^{-2}). The product rule could then be used in such situations, howeve the quotient rule is usually just as easy to apply.

Let’s look at some examples!

Example 1

Let h(x) = \frac{2}{x^4}. As discussed above, we don’t have to use the quotient rule here because the top function is just a constant. Use the quotient rule to find h'(x) anyways, and then verify the result without it.

Using the quotient rule, we have:

    \[ h'(x) = \frac{\diff{}{x} \Big[ 2 \Big] \cdot (x^4) - 2 \cdot \diff{}{x} \Big[ x^4 \Big]}{(x^4)^2} \]

    \[ = \frac{0 \cdot x^4 - 2 \cdot (4x^3)}{x^8} \]

    \[ = \frac{-8x^3}{x^8} = - \frac{8}{x^5} \]

Without the quotient rule, we could simply rewrite the original function as h(x) = 2x^{-4}, and then use the power rule:

    \[ h'(x) = -8 x^{-5} = -\frac{8}{x^5} \]

just like we got otherwise. As you can see, the quotient rule isn’t needed here but still works.

Example 2

Let f(x) = \frac{x^5}{3}. As discussed above, we don’t have to use the quotient rule here because the bottom function is just a constant. Use the quotient rule to find f'(x) anyways, and then verify the result without it.

Using the quotient rule, we have:

    \[ f'(x) = \frac{\diff{}{x} \Big[ x^5 \Big] \cdot (3) - x^5 \cdot \diff{}{x} \Big[ 3 \Big]}{3^2} \]

    \[ = \frac{5x^4 \cdot 3 - x^5 \cdot (0)}{9} = \frac{15x^4}{9} = \frac{5x^4}{3} \]

But remember, the original function was simply f(x) = \frac{1}{3}x^5 whose derivative, according to the power rule (pulling the \frac{1}{3} out), is \frac{5}{3}x^4 just like we got using the quotient rule!

Example 3

I mentioned above that finding the derivative of  \frac{x^2 - 6x+2}{x^3} doesn’t require the quotient rule because the denominator can be distributed into the terms of the numerator. Do this, and then find the derivative. Then use the quotient rule and show that the results are identical.

Distributing the denominator into the terms of the numerator looks like this (try this first!):

    \[ \frac{x^2}{x^3} - \frac{6x}{x^3} + \frac{2}{x^3} \]

    \[ = \frac{1}{x} - \frac{6}{x^2} + \frac{2}{x^3} \]

And now we can clearly take the derivative of the parts individually using the power rule. That becomes

    \[ -\frac{1}{x^2} + \frac{12}{x^3} - \frac{6}{x^4} \]

Now let’s check this using the quotient rule with the original function. That becomes

    \[ \frac{\diff{}{x} \Big[ x^2 - 6x + 2 \Big] \cdot x^3 - (x^2 - 6x + 2) \cdot \diff{}{x} \Big[ x^3 \Big]}{(x^3)^2} \]

    \[ \frac{(2x-6) \cdot x^3 - (x^2 - 6x + 2) \cdot 3x^2}{x^6} \]

    \[ = \frac{2x^4 - 6x^3 - 3x^4 + 18x^3 - 6x^2}{x^6} \]

    \[ = \frac{-x^4 + 12x^3-6x^2}{x^6} \]

And to show that this result is the same, we again distribute the denominator into the terms of the numerator:

    \[ = \frac{-x^4}{x^6} + \frac{12x^3}{x^6} - \frac{6x^2}{x^6} \]

which simplifies to what we got before! Keep this technique in mind so you know some times where you don’t need the quotient rule. Let’s look at some more.

Example 4

Find the derivative of y(t) = \frac{t^2-3}{2t+1}.

We have to use the quotient rule here. We get

    \[ y'(t) = \frac{\diff{}{t} \Big[ t^2-3 \Big] \cdot (2t+1) - (t^2-3) \cdot \diff{}{t} \Big[ 2t+1\Big]}{(2t+1)^2} \]

    \[ = \frac{(2t) \cdot (2t+1) - (t^2 - 3) \cdot (2)}{(2t+1)^2} \]

    \[ = \frac{4t^2 + 2t - 2t^2 + 6}{(2t+1)^2} = \frac{2t^2 + 2t + 6}{(2t+1)^2} \]

The final numerator doesn’t factor, so we’re done here!

Example 5

Compute \diff{y}{x} for y = \frac{12x^2 - 5x}{3x+1}

The quotient rule is as follows:

    \[ \diff{y}{x} = \frac{\diff{}{x} \Big[ 12x^2 - 5x \Big] \cdot (3x+1) - (12x^2 - 5x) \cdot \diff{}{x} \Big[3x+1\Big]}{(3x+1)^2} \]

    \[ = \frac{(24x-5)(3x+1) - (12x^2 - 5x) \cdot 3}{(3x+1)^2} \]

    \[ = \frac{72x^2 + 9x- 5 - 36x^2 + 15x}{(3x+1)^2} \]

    \[ = \frac{36x^2 + 24x - 5}{(3x+1)^2} \]

The numerator of the answer doesn’t factor in a way that cancels a term from the denominator, so we’re done.

More Quotient Rule Examples

The following are more examples of using the product rule with special functions and the chain rule, which are only covered later on in these notes. These problems only apply after you’ve done some future material as well.

Example 6

Find the derivative of y = \frac{x^3}{ \sin{4x}}.

This is clearly a quotient of functions, so we’ll proceed with the quotient rule.

    \[ \diff{y}{x} = \frac{\diff{}{x} \Big[ x^3 \Big] \cdot \sin{4x} - x^3 \cdot \diff{}{x} \Big[ \sin{4x} \Big]}{(\sin{4x})^2} \]

    \[ = \frac{3x^2 \sin{4x} - x^3 \cdot (4\cos{4x})}{\sin ^2{4x}} \]

    \[ = \frac{3x^2 \sin{4x} - 4x^3 \cos{4x}}{\sin ^2{4x}} \]

This is as simplified as is practically necessary, although convince yourself that this is equal to

    \[ = \frac{3x^2 - 4x^3 \cot{4x}}{\sin{4x}} \]

Example 7

Find the derivative of y = \frac{\arctan{x}}{ x^2 + 1}.

We have that

    \[ \diff{y}{x} = \frac{\diff{}{x} \Big[ \arctan{x} \Big] \cdot (x^2 + 1) - \arctan{x} \cdot \diff{}{x} \Big[ x^2 + 1 \Big]}{(\arctan{x} )^2} \]

    \[ = \frac{\frac{1}{x^2+1} \cdot (x^2 + 1) - \arctan{x} \cdot 2x}{(\arctan{x} )^2} \]

    \[ = \frac{1- 2x \arctan{x} }{(\arctan{x} )^2} \]

Example 8

Find the derivative of z = \frac{e^x +1}{ e^x-1}.

We have that

    \[ \diff{z}{x} = \frac{\diff{}{x} \Big[ e^x + 1\Big] \cdot (e^x - 1) - (e^x + 1) \cdot \diff{}{x} \Big[ e^x - 1 \Big]}{(e^x - 1)^2} \]

    \[ \diff{z}{x} = \frac{e^x \cdot (e^x - 1) - (e^x + 1) \cdot e^x }{(e^x - 1)^2} \]

    \[ = \frac{-2e^x}{(e^x - 1)^2} \]

Example 9

Find the derivative of z = \frac{\sqrt{x^2 + 4}}{ 4-\sqrt{x^2 + 4} }.

The derivative is:

    \[ \diff{z}{x} = \frac{\diff{}{x} \Big[\sqrt{x^2 + 4} \Big] \cdot (4-\sqrt{x^2 + 4} ) - \sqrt{x^2 + 4} \cdot \diff{}{x} \Big[ 4-\sqrt{x^2 + 4} \Big]}{(4-\sqrt{x^2 + 4})^2} \]

Now, we will clearly need to find the derivative of \sqrt{x^2 + 4} for two locations in the numerator above, so let’s do that.

    \[ \diff{}{x} \Big[\sqrt{x^2 + 4} \Big] = \frac{1}{2}(x^2 + 4)^{-1/2} \cdot 2x = \frac{x}{\sqrt{x^2+4}} \]

where the factor of 2x comes from the chain rule. We can plug this into the above to continue on:

    \[ \diff{z}{x} = \frac{\frac{x}{\sqrt{x^2+4}} \cdot (4-\sqrt{x^2 + 4} ) - \sqrt{x^2 + 4} \cdot \frac{-x}{\sqrt{x^2+4}}}{(4-\sqrt{x^2 + 4})^2} \]

    \[ = \frac{\frac{4x}{\sqrt{x^2+4}} -x - -x}{(4-\sqrt{x^2 + 4})^2} = \frac{4x}{\sqrt{x^2+4}(4-\sqrt{x^2 + 4})^2} \]

Need more? Here you can get the full version of these notes!